Dalam kehidupan sehari-hari sering kita dihadapkan pada suatu masalah perhitungan yang melibatkan beberapa variable. Sebagai contoh, berapa harga minyak /liter jika yang diketahui adalah harga /tong, atau berapa jumlah bahan bakar yang diperlukan untuk menempuh jarak tertentu, dan sebagainya. Permasalahan tersebut dapat diselesaikan dengan grafik atau dengan system persamaan linier. Namun, akan lebih efisien jika menggunakan system persamaan linier (karena tidak perlu menggambar grafik).
Penyelesaian masalah perhitungan menggunakan system persamaan linier, sebenarnya bukan sesuatu yang baru. Sistem persamaan linier bahkan sudah digunakan sejak 4000 tahun yang lalu (sekitar tahun 2000SM) pada masa Babylonian (Babel).
Hal ini bisa kita lihat dalam tablet YBC 4652 yang menjelaskan bagaimana Babel menyelesaikan suatu masalah dengan persamaan linier. Dalam tablet YBC 4652 dituliskan:
Yang artinya antara lain:
Saya menemukan sebuah batu, (tetapi) tidak menimbang, (setelah) saya menimbang (dari) 8 kali beratnya, ditambah 3 gin, sepertiga dari sepertiga belas dikalikan dengan 21, kemudian (itu) ditambahkan, lalu saya menimbang(nya): 1 ma-na [= 60 gin]. Berapa (berat sesungguhnya) dari batu? Berat asli dari batu itu adalah 4 ½ gin.
Masalah ini dapat diterjemahkan ke dalam persamaan modern, misal berat batu=x, maka:
8x + 3 + 7/13 (8x + 3) = 60
8x + 3 + 56/13x + 21/ 13 = 60
104x + 39 + 56x + 21 = 780
160x = 720
x = 4,5
jadi berat batu = 4,5 gin
Meskipun tablet tidak berisi prosedur penulis (tablet) dalam memecahkan masalah, ternyata terdapat jawaban yang benar dari 4½ . Namun, berdasarkan apa yang kita tahu tentang metode khas Babel 'untuk memecahkan persamaan linier seperti itu, kita dapat berasumsi dengan keyakinan bahwa ahli kitab mungkin menggunakan metode dengan posisi yang salah (Tom Zara dalam Katz,2004).
Kita melihat bahwa kompleks sistem persamaan linier disusun dan dipecahkan, dan Babel menyusun secara sistematis masalah karakter kuadrat dan tentu juga untuk memecahkannya. Semua itu dengan teknik komputasi yang seluruhnya setara dengan kita. Jika ini adalah situasi yang sudah ada di waktu Old Babel, selanjutnya pengembangan nantinya harus melihat dengan pandangan berbeda.
 | |
| Rene Decartes |
Meskipun babel sudah menggunakan Sistem Persamaan Linier dalam kehidupan sehari-hari mereka, namun istilah “Sistem Persamaan Linier (Linear Equation)” sendiri baru muncul sekitar abad ke-17 oleh seorang matematikawan Perancis bernama Rene Decartes. Rene Descartes dilahirkan pada tahun 1596, tanggal 31 Maret di sebuah desa di Prancis. Dia menempuh pendidikan di Belanda dan belajar matematika di waktu luang, karya Descartes yang paling menghargai adalah pengembangannya geometri Cartesian yang menggunakan aljabar untuk menggambarkan geometri. Kemungkinan, Descartes menemukan istilah untuk “Sistem Persamaan Linier (Linear Equation)” ketika dia belajar di Belanda.
Meskipun penggunaan Masalah tablet yang dapat diterjemahkan ke dalam persamaan kuadrat tidak ditemukan sampai abad kedua puluh, tablet berisi masalah persamaan kuadrat benar-benar melebihi yang mengandung masalah linear (Tom Zara Katz, 2004). Bahkan, mulai dari awal 2000 SM, Babel mampu memecahkan sistem persamaan dalam bentuk
x + y = p
xy = q
Jika kita menyelesaikan persamaan kedua untuk y (yang menghasilkan persamaan y = q / x), pengganti nilai ini (q / x) untuk y dalam persamaan pertama (yang memberi kami x + (q / x) = p), dan kemudian kalikan semua istilah dalam persamaan ini direvisi oleh x, kita mendapatkan yang setara kuadrat persamaan
x2 + q = px
Dalam Introduction to the Analysis of Algebraic Curves of 1750, diterbitkan aturan namanya untuk solusi dari suatu n × sistem n, tapi ia tidak memberikan bukti. Ia dibawa untuk belajar sistem persamaan linier ketika mencoba untuk memecahkan masalah geometri, determinan kurva aljabar n derajat melewati (1 / 2) n 2 2 + (3 / 2) n titik tetap. Itu yang pertama untuk mengamati bahwa sistem persamaan n di n tidak diketahui tidak selalu memiliki solusi yang unik, untuk mendapatkan keunikan itu diperlukan untuk menambahkan kondisi.
Pada abad kedelapan belas tidak ada studi tentang persamaan linier tentang determinan, sehingga tidak ada pertimbangan diberikan untuk sistem di mana jumlah persamaan berbeda dari jumlah tidak diketahui. Sehubungan dengan penemuan tentang metode kuadrat terkecil (diterbitkan dalam a paper in 1811 dealing with the determination of the orbit of an asteroid), Gauss paper pada tahun 1811 berkaitan dengan penentuan orbit asteroid), memperkenalkan prosedur yang sistematis, dan sekarang disebut eliminasi Gaus untuk solusi sistem persamaan linier.
Metode eliminasi Gauss muncul di Bab Delapan, Rectangular Array, dari matematika teks Jiuzhang Cina suanshu penting atau Sembilan Bab di Seni Matematika . Penggunaannya diilustrasikan dalam masalah delapan belas, dengan 2-5 persamaan. Referensi pertama buku dengan judul ini adalah tanggal untuk 179 CE, tapi bagian itu ditulis pada awal sekitar 150 SM. Hal ini dikomentari oleh Liu Hui di abad ke-3.
Metode di Eropa berasal dari catatan Isaac Newton. Pada 1670, ia menulis bahwa semua buku aljabar yang diketahui olehnya kekurangan pelajaran untuk memecahkan persamaan simultan, yang Newton kemudian disediakan. Universitas Cambridge akhirnya diterbitkan catatan sebagai Arithmetica Universalis tahun 1707 lama setelah Newton meninggalkan kehidupan akademik. Catatan itu secara luas ditiru, yang membuat (apa yang sekarang disebut) eliminasi Gauss pelajaran standar dalam buku teks aljabar pada akhir abad ke-18. Carl Friedrich Gauss pada tahun 1810 menyusun notasi untuk eliminasi simetrik yang diadopsi pada abad ke-19 oleh komputer tangan profesional untuk memecahkan persamaan normal masalah kuadrat-terkecil. Algoritma yang diajarkan di sekolah tinggi bernama untuk Gauss hanya pada 1950-an sebagai akibat dari kebingungan sejarah subjek.
Metode eliminasi Gauss kurang efisien untuk menyelesaikan sebuah SPL, namun pada perkembangannya metode ini disempurnakan menjadi eliminasi Gauss-Jordan
Motede tersebut dinamai Eliminasi Gauss-Jordan untuk menghormati Carl Friedrich Gauss dan Whilhelm Jordan.
Wilhelm Jordan (1842-1899) adalah seorang insinyur Jerman yang ahli dalam bidang geodesi. Sumbangannya untuk penyelesaian sistem linear dalam buku populernya, Handbuch de Vermessungskunde (Buku panduan Geodesi) pada tahun 1988.
Aplikasi untuk mencari Invers
Jika eliminasi Gauss-Jordan diterapkan dalam matriks persegi, metode tersebut dapat digunakan untuk menghitung invers dari matriks. Eliminasi Gauss-Jordan hanya dapat dilakukan dengan menambahkan dengan matriks identitas dengan dimensi yang sama, dan melalui operasi-operasi matriks:
Jika A contoh matriks persegi yang diberikan:
Kemudian, setelah ditambahkan dengan matriks identitas:
Dengan melakukan operasi baris dasar pada matriks[AI] sampai A menjadi matriks identitas, maka didapatkan hasil akhir:
Thomas (1984:93-94) mengatakan bahwa setiap matriks memiliki bentuk eselon baris tereduksi yang unik, artinya kita akan memperoleh bentuk eselon baris tereduksi yang sama untuk matriks tertentu bagaimanapun variasi operasi baris yang dilakukan.
DAFTAR PUSTAKA
Zara, Tom.2008. A Brief Study of Some Aspects of Babylonian Mathematics.United State: Liberty University Spring
Hodgkin, Luke.2005.A History of Mathematics.UK:Oxford
Lipschutz, Seymour, and Lipson, Mark. “Schaum’s Outlines: Linear Algebra“. Tata McGraw-hill edition. Delhi 2001. pp. 69-80.
Strang, Gilbert (2003). Introduction to Linear Algebra, 3rd edition, Wellesley, Massachusetts: Wellesley-Cambridge Press, 74-76.
Sahid. Pengantar Komputasi Numerik dengan MATLAB. 2005. Yogyakarta:ANDI





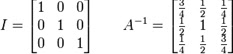
lengkap ta ini?????
BalasHapusYg gk dapet Bansos ketik 1
BalasHapus