suka_suka_gue: Vector-valued function

A vector-valued function also referred to as a vector function is a mathematical function of one or more variables whose range is a set of multidimensional vectors or infinite-dimensional vectors. Often the input of a vector-valued function is a scalar, but in general the input can be a vector of both complex or real variables.

[hide]

[edit] Example

A common example of a vector valued function is one that depends on a single real number parameter t, often representing time, producing a vector v(t) as the result. In terms of the standard unit vectors i, j, k of Cartesian 3-space, these specific type of vector-valued functions are given by expressions such as

$\mathbf{r}(t)=f(t)\mathbf{i}+g(t)\mathbf{j}$ or
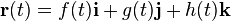
$\mathbf{r}(t)=f(t)\mathbf{i}+g(t)\mathbf{j}+h(t)\mathbf{k}$

where f(t), g(t) and h(t) are the coordinate functions of the parameter t. The vector r(t) has its tail at the origin and its head at the coordinates evaluated by the function.
The vector shown in the graph to the right is the evaluation of the function near t=19.5 (between 6π and 6.5π; i.e., somewhat more than 3 rotations). The spiral is the path traced by the tip of the vector as t increases from zero through 8π.
Vector functions can also be referred to in a different notation:

$\mathbf{r}(t)=\langle f(t), g(t)\rangle$ or
$\mathbf{r}(t)=\langle f(t), g(t), h(t)\rangle$

[edit] Properties

The domain of a vector-valued function is the intersection of the domain of the functions f, g, and h.

[edit] Derivative of a three-dimensional vector function

Many vector-valued functions, like scalar-valued functions, can be differentiated by simply differentiating the components in the Cartesian coordinate system. Thus, if

$\mathbf{r}(t) = f(t)\mathbf{i} + g(t)\mathbf{j} + h(t)\mathbf{k}$

is a vector-valued function, then

$\frac{d\mathbf{r}(t)}{dt} = f'(t)\mathbf{i} + g'(t)\mathbf{j} + h'(t)\mathbf{k}.$

The vector derivative admits the following physical interpretation: if r(t) represents the position of a particle, then the derivative is the velocity of the particle

$\mathbf{v}(t) = \frac{d\mathbf{r}(t)}{dt} .$

Likewise, the derivative of the velocity is the acceleration

$\frac{d\bold{v}(t)}{d t}=\bold{a}(t).$

[edit] Partial derivative

The partial derivative of a vector function a with respect to a scalar variable q is defined as^[1]

$\frac{\partial\mathbf{a}}{\partial q} = \sum_{i=1}^{3}\frac{\partial a_i}{\partial q}\mathbf{e}_i$

where a_i is the scalar component of a in the direction of e_i. It is also called the direction cosine of a and e_i or their dot product. The vectors e₁,e₂,e₃ form an orthonormal basis fixed in the reference frame in which the derivative is being taken.

[edit] Ordinary derivative

If a is regarded as a vector function of a single scalar variable, such as time t, then the equation above reduces to the first ordinary time derivative of a with respect to t,^[1]

$\frac{d\mathbf{a}}{dt} = \sum_{i=1}^{3}\frac{da_i}{dt}\mathbf{e}_i.$

[edit] Total derivative

If the vector a is a function of a number n of scalar variables q_r (r = 1,...,n), and each q_r is only a function of time t, then the ordinary derivative of a with respect to t can be expressed, in a form known as the total derivative, as^[1]

$\frac{d\mathbf a}{dt} = \sum_{r=1}^{n}\frac{\partial \mathbf a}{\partial q_r} \frac{dq_r}{dt} + \frac{\partial \mathbf a}{\partial t}.$

Some authors prefer to use capital D to indicate the total derivative operator, as in D/Dt. The total derivative differs from the partial time derivative in that the total derivative accounts for changes in a due to the time variance of the variables q_r.

[edit] Reference frames

Whereas for scalar-valued functions there is only a single possible reference frame, to take the derivative of a vector-valued function requires the choice of a reference frame (at least when a fixed Cartesian coordinate system is not implied as such). Once a reference frame has been chosen, the derivative of a vector-valued function can be computed using techniques similar to those for computing derivatives of scalar-valued functions. A different choice of reference frame will, in general, produce a different derivative function. The derivative functions in different reference frames have a specific kinematical relationship.

[edit] Derivative of a vector function with nonfixed bases

The above formulas for the derivative of a vector function rely on the assumption that the basis vectors e₁,e₂,e₃ are constant, that is, fixed in the reference frame in which the derivative of a is being taken, and therefore the e₁,e₂,e₃ each has a derivative of identically zero. This often holds true for problems dealing with vector fields in a fixed coordinate system, or for simple problems in physics. However, many complex problems involve the derivative of a vector function in multiple moving reference frames, which means that the basis vectors will not necessarily be constant. In such a case where the basis vectors e₁,e₂,e₃ are fixed in reference frame E, but not in reference frame N, the more general formula for the ordinary time derivative of a vector in reference frame N is^[1]

$\frac{{}^\mathrm{N}d\mathbf{a}}{dt} = \sum_{i=1}^{3}\frac{da_i}{dt}\mathbf{e}_i + \sum_{i=1}^{3}a_i\frac{{}^\mathrm{N}d\mathbf{e}_i}{dt}$

where the superscript N to the left of the derivative operator indicates the reference frame in which the derivative is taken. As shown previously, the first term on the right hand side is equal to the derivative of a in the reference frame where e₁,e₂,e₃ are constant, reference frame E. It also can be shown that the second term on the right hand side is equal to the relative angular velocity of the two reference frames cross multiplied with the vector a itself.^[1] Thus, after substitution, the formula relating the derivative of a vector function in two reference frames is^[1]

$\frac{{}^\mathrm Nd\mathbf a}{dt} = \frac{{}^\mathrm Ed\mathbf a }{dt} + {}^\mathrm N \mathbf \omega^\mathrm E \times \mathbf a$

where ^Nω^E is the angular velocity of the reference frame E relative to the reference frame N.
One common example where this formula is used is to find the velocity of a space-borne object, such as a rocket, in the inertial reference frame using measurements of the rocket's velocity relative to the ground. The velocity ^Nv^R in inertial reference frame N of a rocket R located at position r^R can be found using the formula

$\frac{{}^\mathrm Nd}{dt}(\mathbf r^\mathrm R) = \frac{{}^\mathrm Ed}{dt}(\mathbf r^\mathrm R) + {}^\mathrm N \mathbf \omega^\mathrm E \times \mathbf r^\mathrm R.$

where ^Nω^E is the angular velocity of the Earth relative to the inertial frame N. Since velocity is the derivative of position, ^Nv^R and ^Ev^R are the derivatives of r^R in reference frames N and E, respectively. By substitution,

${}^\mathrm N \mathbf v^\mathrm R = {}^\mathrm E \mathbf v^\mathrm R + {}^\mathrm N \mathbf \omega^\mathrm E \times \mathbf r^\mathrm R$

where ^Ev^R is the velocity vector of the rocket as measured from a reference frame E that is fixed to the Earth.

[edit] Derivative and vector multiplication

The derivative of the products of vector functions behaves similarly to the derivative of the products of scalar functions.^[2] Specifically, in the case of scalar multiplication of a vector, if p is a scalar variable function of q,^[1]

$\frac{\partial}{\partial q}(p\mathbf a) = \frac{\partial p}{\partial q}\mathbf a + p\frac{\partial \mathbf a}{\partial q}.$

In the case of dot multiplication, for two vectors a and b that are both functions of q,^[1]

$\frac{\partial}{\partial q}(\mathbf a \cdot \mathbf b) = \frac{\partial \mathbf a }{\partial q} \cdot \mathbf b + \mathbf a \cdot \frac{\partial \mathbf b}{\partial q}.$

Similarly, the derivative of the cross product of two vector functions is^[1]

$\frac{\partial}{\partial q}(\mathbf a \times \mathbf b) = \frac{\partial \mathbf a }{\partial q} \times \mathbf b + \mathbf a \times \frac{\partial \mathbf b}{\partial q}.$

[edit] Derivative of an n-dimensional vector function

A function f of a real number t with values in the space

R n

can be written as $f(t)=(f_1(t),f_2(t),\ldots,f_n(t))$ . Its derivative equals

$f'(t)=(f_1'(t),f_2'(t),\ldots,f_n'(t))$ .

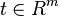If f is a function of several variables, say of $t\in R^m$ , then the partial derivatives of the components of f form a $n\times m$ matrix called the Jacobian matrix of f.

[edit] Infinite-dimensional vector functions

If the values of a function f lie in an infinite-dimensional vector space X, such as a Hilbert space, then f may be called an infinite-dimensional vector function.

[edit] Functions with values in a Hilbert space

If the argument of f is a real number and X is a a Hilbert space, then the derivative of f at a point t can be defined as in the finite-dimensional case: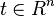

$f'(t)=\lim_{h\rightarrow0}\frac{f(t+h)-f(t)}{h}.$

Most results of the finite-dimensional case also hold in the infinite-dimensional case too, mutatis mutandis. Differentiation can also be defined to functions of several variables (e.g., $t\in R^n$ or even $t\in Y$ , where Y is an infinite-dimensional vector space).
N.B. If X is a Hilbert space, then one can easily show that any derivative (and any other limit) can be computed componentwise: if

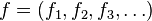
$f=(f_1,f_2,f_3,\ldots)$

(i.e., $f=f_1 e_1+f_2 e_2+f_3 e_3+\cdots$ , where $e_1,e_2,e_3,\ldots$ is an orthonormal basis of the space X), and

f'(t)

exists, then

$f'(t)=(f_1'(t),f_2'(t),f_3'(t),\ldots)$ .

However, the existence of a componentwise derivative does not guarantee the existence of a derivative, as componentwise convergence in a Hilbert space does not guarantee convergence with respect to the actual topology of the Hilbert space.

[edit] Other infinite-dimensional vector spaces

Most of the above hold for other topological vector spaces X too. However, not as many classical results hold in the Banach space setting, e.g., an absolutely continuous function with values in a suitable Banach space need not have a derivative anywhere. Moreover, in most Banach spaces setting there are no orthonormal bases.

suka_suka_gue

search this blog

Senin, 25 Oktober 2010

Vector-valued function

Contents